1 5 Solving Inequalities Answers

1.five: Solve Inequalities

Last updated
Save as PDF

Page ID: 51443

Learning Objectives

Draw solutions to inequalities
- Represent inequalities on a number line
- Correspond inequalities using interval note
Solve single-step inequalities
- Utilise the improver and multiplication properties to solve algebraic inequalities and express their solutions graphically and with interval notation
- Solve inequalities that contain absolute value
Solve multi-step inequalities
- Combine backdrop of inequality to isolate variables, solve algebraic inequalities, and limited their solutions graphically
- Simplify and solve algebraic inequalities using the distributive property to clear parentheses and fractions

Represent inequalities on a number line

First, let'southward define some important terminology. An inequality is a mathematical statement that compares 2 expressions using the ideas of greater than or less than. Special symbols are used in these statements. When you read an inequality, read it from left to right—merely similar reading text on a page. In algebra, inequalities are used to describe big sets of solutions. Sometimes in that location are an space corporeality of numbers that volition satisfy an inequality, so rather than try to list off an infinite amount of numbers, we accept developed some ways to draw very big lists in succinct ways.

The commencement fashion you are probably familiar with—the bones inequality. For instance:

${x}\lt{nine}$ or try to listing all the possible numbers that are less than 9? (hopefully, your answer is no)
$-5$.

Note how placing the variable on the left or right of the inequality sign can change whether you are looking for greater than or less than.

For example:

$x\lt5$ ways all the real numbers that are less than 5, whereas;
$x\gt{5}$ note how the inequality is however pointing the aforementioned direction relative to ten. This statement represents all the real numbers that are greater than v, which is easier to interpret than five is less than ten.

The 2d style is with a graph using the number line:

$A numberline. It is a long horizontal line with evenly spaced points, the middle of which is zero.$

And the third mode is with an interval.

We will explore the second and third means in depth in this section. Once again, those iii ways to write solutions to inequalities are:

an inequality
an interval
a graph

Inequality Signs

The box below shows the symbol, meaning, and an example for each inequality sign. Sometimes it'southward piece of cake to get tangled upward in inequalities, simply remember to read them from left to right.

Symbol	Words	Example
${2}\neq{viii}$, two is not equal to 8.
${5}\gt{ane}$, five is greater than 1
${2}\lt{xi}$, 2 is less than 11
${4}\geq{ iv}$, 4 is greater than or equal to 4
${7}\leq{ix}$, seven is less than or equal to 9

The inequality ${y}<{x}$. The sides of any inequality can be switched every bit long equally the inequality symbol between them is as well reversed.

Graphing an Inequality

Inequalities tin likewise be graphed on a number line. Beneath are three examples of inequalities and their graphs. Graphs are a very helpful way to visualize data – especially when that information represents an infinite listing of numbers!

$x\leq -4$. This translates to all the real numbers on a number line that are less than or equal to iv.

$Number line. Shaded circle on negative 4. Shaded line through all numbers less than negative 4.$

${x}\geq{-3}$. This translates to all the real numbers on the number line that are greater than or equal to -three.

$Number line. Shaded circle on negative 3. Shaded line through all numbers greater than negative 3.$

Each of these graphs begins with a circle—either an open up or closed (shaded) circumvolve. This point is often chosen the end bespeak of the solution. A closed, or shaded, circle is used to represent the inequalities greater than or equal to $\displaystyle \left(\leq\right)$. The point is part of the solution. An open circle is used for greater than (>) or less than (<). The point is non part of the solution.

The graph then extends endlessly in 1 management. This is shown by a line with an arrow at the finish. For example, detect that for the graph of $−3$, represented with a closed circle since the inequality is greater than or equal to$−iii$. The arrow at the end indicates that the solutions keep infinitely.

Example

Graph the inequality $x\ge 4$
[reveal-answer q="797241″]Show Solution[/reveal-answer]
[hidden-respond a="797241″]

We tin employ a number line as shown. Because the values for x include 4, we place a solid dot on the number line at 4.

So nosotros describe a line that begins at $x=4$ and, every bit indicated by the arrowhead, continues to positive infinity, which illustrates that the solution set up includes all real numbers greater than or equal to four.
$A number line starting at zero with the last tick mark being labeled 11. There is a dot at the number 4 and an arrow extends toward the right.$

[/hidden-answer]

This video shows an example of how to draw the graph of an inequality.

$Thumbnail for the embedded element "Graph Linear Inequalities in One Variable (Basic)"$

A YouTube element has been excluded from this version of the text. You lot can view it online here: pb.libretexts.org/ba/?p=52

Example

Write an inequality describing all the real numbers on the number line that are less than 2, then draw the corresponding graph.
[reveal-reply q="867890″]Show Solution[/reveal-reply]
[subconscious-reply a="867890″]

We need to start from the left and piece of work right, so we start from negative infinity and finish at $-ii$.

Inequality: $x<2$

To draw the graph, place an open dot on the number line first, then draw a line extending to the left. Describe an arrow at the leftmost signal of the line to signal that information technology continues for infinity.

$Number line. Unshaded circle around 2 and shaded line through all numbers less than 2.$

[/subconscious-answer]

The following video shows how to write an inequality mathematically when information technology is given in words. Nosotros will then graph information technology.

$Thumbnail for the embedded element "Given Interval in Words, Graph and Give Inequality"$

A YouTube element has been excluded from this version of the text. You tin can view it online hither: pb.libretexts.org/ba/?p=52

Represent inequalities using interval notation

Some other commonly used, and arguably the most curtailed, method for describing inequalities and solutions to inequalities is called interval notation. With this convention, sets are built with parentheses or brackets, each having a singled-out pregnant. The solutions to $\left[4,\infty \right)$. This method is widely used and volition exist present in other math courses you lot may accept.

The principal concept to retrieve is that parentheses stand for solutions greater or less than the number, and brackets represent solutions that are greater than or equal to or less than or equal to the number. Apply parentheses to represent infinity or negative infinity, since positive and negative infinity are not numbers in the usual sense of the word and, therefore, cannot be "equaled." A few examples of an interval, or a set up of numbers in which a solution falls, are $-two$ and $-two$, but non including $\left(-1,0\right)$, all real numbers betwixt, but not including $0$; and $1$. The tabular array below outlines the possibilities. Remember to read inequalities from left to right, simply like text.

The table beneath describes all the possible inequalities that can occur and how to write them using interval annotation, where a and b are real numbers.

Inequality	Words	Interval Notation
$\left(a,b\right)$
$\left(a,\infty \correct)$
$\left(-\infty ,b\correct)$
$\left[a,\infty \correct)$
$\left(-\infty ,b\right]$
$\left[a,b\right)$
$\left(a,b\right]$
$\left[a,b\right]$
$\left(-\infty ,a\right)\cup \left(b,\infty \right)$
All existent numbers	All real numbers	$\left(-\infty ,\infty \correct)$

Example

Draw the inequality $x\ge 4$ using interval annotation
[reveal-reply q="817362″]Testify Solution[/reveal-answer]
[hidden-answer a="817362″]

The solutions to $\left[4,\infty \right)$.

Note the use of a bracket on the left because iv is included in the solution set.

[/subconscious-answer]

In the following video we show another example of using interval notation to draw an inequality.

$Thumbnail for the embedded element "Given an Inequality, Graph and Give Interval Notation"$

A YouTube chemical element has been excluded from this version of the text. Y'all tin view it online hither: pb.libretexts.org/ba/?p=52

Example

Utilize interval notation to indicate all real numbers greater than or equal to $-two$.
[reveal-respond q="961990″]Show Solution[/reveal-answer]
[hidden-answer a="961990″]

Use a subclass on the left of $\left[-2,\infty \correct)$. The bracket indicates that $-2$ to infinity.

[/hidden-answer]

In the following video we bear witness another example of translating words into an inequality and writing it in interval notation, also as drawing the graph.

$Thumbnail for the embedded element "Given Interval in Words, Graph and Give Interval Notation"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

Think Nearly It

In the previous examples you were given an inequality or a clarification of one with words and asked to draw the corresponding graph and write the interval. In this instance you are given an interval and asked to write the inequality and draw the graph.

Given $\left(-\infty,10\right)$, write the associated inequality and depict the graph.

In the box below, write downward whether you lot call back it will be easier to draw the graph first or write the inequality first.

[practice-expanse rows="1″][/practice-area]
[reveal-reply q="15120″]Testify Solution[/reveal-answer]

[hidden-answer a="15120″]

Nosotros will depict the graph first.

The interval reads "all real numbers less than 10," so we will start by placing an open dot on 10 and drawing a line to the left with an arrow indicating the solution continues to negative infinity.

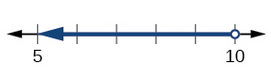
$An open circle on 10 and a line going from 10 to all numbers below 10.$

To write the inequality, nosotros volition use < since the parentheses indicate that 10 is not included. $x<ten$

[/subconscious-answer]

In the following video, you will see examples of how to describe a graph given an inequality in interval notation.

$Thumbnail for the embedded element "Given Interval Notation, Graph and Give Inequality"$

A YouTube chemical element has been excluded from this version of the text. Y'all can view it online here: pb.libretexts.org/ba/?p=52

And finally, one last video that shows how to write inequalities using a graph, with interval note and as an inequality.

$Thumbnail for the embedded element "Ex: Graph Basic Inequalities and Express Using Interval Notation"$

A YouTube element has been excluded from this version of the text. Yous can view it online here: pb.libretexts.org/ba/?p=52

Solve Single-Footstep Inequalities

Solve inequalities with addition and subtraction

You can solve most inequalities using changed operations as you lot did for solving equations. This is because when you add or subtract the same value from both sides of an inequality, you lot have maintained the inequality. These properties are outlined in the box below.

Addition and Subtraction Properties of Inequality

If $a+c>b+c$.

If $a−c>b−c$.

Considering inequalities have multiple possible solutions, representing the solutions graphically provides a helpful visual of the situation, every bit we saw in the last section. The example below shows the steps to solve and graph an inequality and express the solution using interval notation.

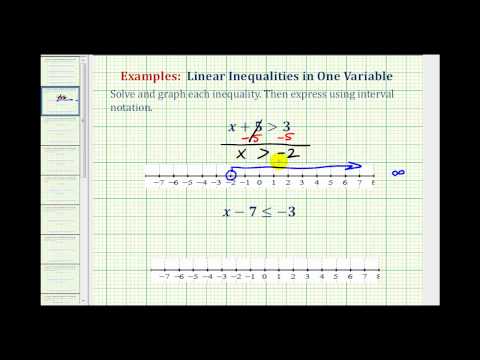
Example

Solve for ten.

${ten}+3\lt{five}$

[reveal-respond q="952771″]Show Solution[/reveal-answer]
[hidden-reply a="952771″]

It is helpful to think of this inequality as asking you to discover all the values for x, including negative numbers, such that when yous add three y'all will become a number less than 5.

$\displaystyle \brainstorm{assortment}{l}x+three<\,\,\,\,v\\\underline{\,\,\,\,\,-three\,\,\,\,-3}\\x\,\,\,\,\,\,\,\,<\,\,\,\,two\,\,\cease{array}$

Isolate the variable past subtracting three from both sides of the inequality.

Reply

Inequality: $x<2$

Interval: $\left(-\infty, 2\right)$

Graph: $Number line. Open circle around 2. Shaded line through all numbers less than 2.$ [/hidden-answer]

The line represents all the numbers to which you tin can add 3 and get a number that is less than 5. There's a lot of numbers that solve this inequality!

Only as you tin can check the solution to an equation, you tin cheque a solution to an inequality. Kickoff, yous check the cease point by substituting it in the related equation. And then yous cheque to see if the inequality is correct by substituting any other solution to meet if it is one of the solutions. Because there are multiple solutions, information technology is a expert practice to check more than one of the possible solutions. This can also help you cheque that your graph is correct.

The example beneath shows how you could cheque that $x+3<5$.

Instance

Bank check that $10+three<5$.

[reveal-answer q="811564″]Show Solution[/reveal-respond]
[hidden-respond a="811564″]

Substitute the stop point 2 into the related equation, $x+3=5$.

$\begin{array}{r}x+iii=5 \\ ii+three=5 \\ 5=five\finish{array}$

Pick a value less than two, such as 0, to bank check into the inequality. (This value will exist on the shaded part of the graph.)

$Number line. Open circle around 2. Shaded line through all numbers less than 2.$

$\displaystyle \brainstorm{array}{r}x+3<5 \\ 0+iii<5 \\ 3<5\finish{array}$

It checks!

$x+3<v$.[/hidden-answer]

The following examples show inequality problems that include operations with negative numbers. The graph of the solution to the inequality is too shown. Remember to check the solution. This is a good habit to build!

Instance

Solve for x: $10-10\leq-12$
[reveal-answer q="815894″]Show Solution[/reveal-respond]
[subconscious-answer a="815894″]

Isolate the variable by adding 10 to both sides of the inequality.

$\displaystyle \brainstorm{array}{r}x-10\le -12\\\underline{\,\,\,+ten\,\,\,\,\,+10}\\x\,\,\,\,\,\,\,\,\,\,\le \,\,\,-2\end{array}$

Answer

Inequality: $\left(-\infty,-2\right]$
Graph: Find that a closed circle is used because the inequality is "less than or equal to" $−two$ because these are the values that are less than $−two$.
$Number line, closed circle on negative 2 and line drawn through all numbers less than negative 2$

[/hidden-reply]

Check the solution to $ten-x\leq -12$
[reveal-reply q="268062″]Show Solution[/reveal-reply]
[hidden-respond a="268062″]

Substitute the finish betoken $x-10=−12$

$\displaystyle \brainstorm{array}{r}x-ten=-12\,\,\,\\\text{Does}\,\,\,-two-10=-12?\\-12=-12\,\,\,\finish{assortment}$

Pick a value less than $−five$, to check in the inequality. (This value will be on the shaded part of the graph.)

$\displaystyle \begin{array}{r}x-ten\le -12\,\,\,\\\text{ }\,\text{ Is}\,\,-v-ten\le -12?\\-15\le -12\,\,\,\\\text{It}\,\text{checks!}\stop{assortment}$

$x-x\leq -12$

[/hidden-answer]

Instance

Solve for a. $a-17>-17$
[reveal-respond q="343031″]Prove Solution[/reveal-respond]
[hidden-answer a="343031″]

Isolate the variable by calculation 17 to both sides of the inequality.

$\displaystyle \begin{array}{r}a-17>-17\\\underline{\,\,\,+17\,\,\,\,\,+17}\\a\,\,\,\,\,\,\,\,\,\,\,>\,\,\,\,\,\,0\stop{array}$

Answer

Inequality: $\displaystyle a\,\,>\,0$

Interval: $\left(0,\infty\right)$ Annotation how we use parentheses on the left to show that the solution does non include 0.

Graph: Note the open circle to prove that the solution does non include 0.

$Number line. Open circle on zero. Highlight through all numbers above zero.$

[/hidden-answer]

Bank check the solution to $a-17>-17$
[reveal-answer q="653357″]Bear witness Solution[/reveal-answer]
[hidden-answer a="653357″]

Is $a-17>-17$?

Substitute the end point 0 into the related equation.

$\displaystyle \brainstorm{array}{r}a-17=-17\,\,\,\\\text{Does}\,\,\,0-17=-17?\\-17=-17\,\,\,\terminate{array}$

Pick a value greater than 0, such as xx, to cheque in the inequality. (This value will exist on the shaded function of the graph.)

$\displaystyle \brainstorm{array}{r}a-17>-17\,\,\,\\\text{Is }\,\,20-17>-17?\\3>-17\,\,\,\\\\\text{It checks!}\,\,\,\,\end{array}$

$a-17>-17$

[/hidden-answer]

The previous examples showed you how to solve a one-step inequality with the variable on the left hand side. The following video provides examples of how to solve the same type of inequality.

$Thumbnail for the embedded element "Ex: Solving One Step Inequalities by Adding and Subtracting (Variable Left Side)"$

A YouTube element has been excluded from this version of the text. You can view it online hither: atomic number 82.libretexts.org/ba/?p=52

What would you do if the variable were on the right side of the inequality? In the post-obit instance, you volition run across how to handle this scenario.

Example

Solve for ten: $4\geq{x}+5$
[reveal-respond q="815893″]Show Solution[/reveal-answer]
[subconscious-answer a="815893″]

Isolate the variable by adding x to both sides of the inequality.

$\displaystyle \begin{array}{r}4\geq{x}+v \\\underline{\,\,\,-5\,\,\,\,\,-five}\\-one\,\,\,\,\,\,\,\,\,\,\ge \,\,\,ten\terminate{array}$

Rewrite the inequality with the variable on the left – this makes writing the interval and drawing the graph easier.

$x\le{-1}$

Annotation how the the pointy role of the inequality is still directed at the variable, so instead of reading as negative one is greater or equal to x, it at present reads as 10 is less than or equal to negative one.

Reply

Inequality: $\left(-\infty,-i\right]$
Graph: Notice that a closed circumvolve is used because the inequality is "less than or equal to" . The blue pointer is drawn to the left of the point $−1$.
$(-oo,-1]$

[/hidden-answer]

Bank check the solution to $4\geq{ten}+5$
[reveal-respond q="568062″]Prove Solution[/reveal-answer]
[subconscious-respond a="568062″]

Substitute the stop bespeak $4=x+5$

$\displaystyle \brainstorm{array}{r}4=x+5\,\,\,\\\text{Does}\,\,\,four=-one+5?\\-ane=-1\,\,\,\stop{array}$

Choice a value less than $−5$, to check in the inequality. (This value volition exist on the shaded part of the graph.)

$\displaystyle \begin{assortment}{r}4\geq{-5}+5\,\,\,\\\text{ }\,\text{ Is}\,\,4\ge 0?\\\text{It}\,\text{checks!}\end{assortment}$

$4\geq{10}+5$[/hidden-answer]

The following video evidence examples of solving inequalities with the variable on the right side.

$Thumbnail for the embedded element "Ex: Solving One Step Inequalities by Adding and Subtracting (Variable Right Side)"$

A YouTube element has been excluded from this version of the text. You lot can view it online hither: pb.libretexts.org/ba/?p=52

Solve inequalities with multiplication and division

Solving an inequality with a variable that has a coefficient other than 1 commonly involves multiplication or division. The steps are like solving one-step equations involving multiplication or partition EXCEPT for the inequality sign. Let's look at what happens to the inequality when y'all multiply or divide each side by the aforementioned number.

Let's start with the true statement: $10>5$
Next, multiply both sides by the same positive number: $x\cdot-2>5 \\ \,\,\,\,\,\cdot -two\,\cdot-two$
xx is greater than 10, so you still have a truthful inequality: $−20$ is not greater than $−20>−x$
When y'all multiply by a positive number, leave the inequality sign as it is!	Y'all must "contrary" the inequality sign to make the statement true: $−20<−10$

$Caution$ Caution! When you multiply or carve up past a negative number, "reverse" the inequality sign. Whenever you multiply or split up both sides of an inequality by a negative number, the inequality sign must be reversed in guild to proceed a truthful statement. These rules are summarized in the box below.

Multiplication and Sectionalization Properties of Inequality

Outset With	Multiply By	Final Inequality
$c$	$a>b$	$ac<bc$

Get-go With	Dissever By	Last Inequality
$c$	$a>b$	$\displaystyle \frac{a}{c}<\frac{b}{c}$

Keep in mind that yous just change the sign when yous are multiplying and dividing by a negative number. If you add together or subtract by a negative number, the inequality stays the aforementioned.

Example

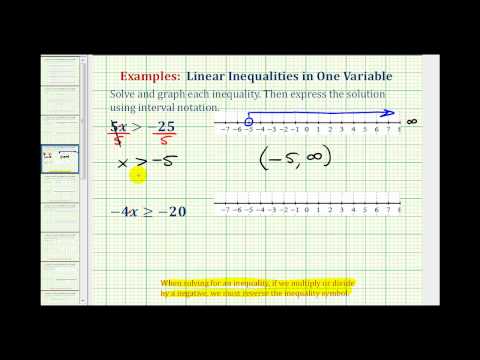
Solve for x. $3x>12$

[reveal-answer q="691711″]Show Solution[/reveal-reply]
[hidden-reply a="691711″]Split both sides by 3 to isolate the variable.

$\displaystyle \brainstorm{assortment}{r}\underline{3x}>\underline{12}\\three\,\,\,\,\,\,\,\,\,\,\,\,three\\x>4\,\,\,\terminate{assortment}$

Check your solution by commencement checking the end point 4, and then checking another solution for the inequality.

$\begin{assortment}{r}iii\cdot4=12\\12=12\\3\cdot10>12\\30>12\\\text{It checks!}\end{assortment}$

Answer

Inequality: $\displaystyle x>4$

Interval: $\left(4,\infty\right)$

Graph: $Number line. Open circle on 4. Highlight through all numbers greater than 4.$

[/hidden-answer]

At that place was no demand to make any changes to the inequality sign because both sides of the inequality were divided by positive iii. In the next instance, there is division by a negative number, so in that location is an additional step in the solution!

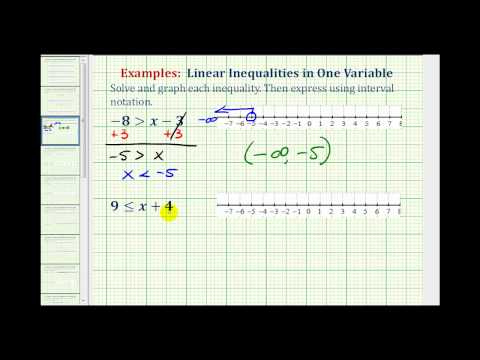
Example

Solve for x. $−2x>6$

[reveal-answer q="604033″]Show Solution[/reveal-answer]
[hidden-answer a="604033″]Divide each side of the inequality by $−2$ to isolate the variable, and change the direction of the inequality sign because of the partition by a negative number.

$\displaystyle \begin{assortment}{r}\underline{-2x}<\underline{\,6\,}\\-ii\,\,\,\,-2\,\\x<-iii\cease{array}$

Check your solution by offset checking the end point $−3$, and so checking another solution for the inequality.

$\begin{array}{r}-2\left(-iii\right)=half-dozen \\6=6\\ -2\left(-6\right)>vi \\ 12>half dozen\terminate{array}$

It checks!

Answer

Inequality: $\displaystyle 10<-iii$

Interval: $\left(-\infty, -3\correct)$

Graph: $−ii$, the inequality symbol was switched from > to <.
[/subconscious-respond]

The following video shows examples of solving 1 footstep inequalities using the multiplication property of equality where the variable is on the left hand side.

$Thumbnail for the embedded element "Ex: Solve One Step Linear Inequality by Dividing (Variable Left)"$

A YouTube chemical element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=52

Think About It

Earlier you read the solution to the adjacent case, think about what backdrop of inequalities you may need to use to solve the inequality. What is dissimilar about this example from the previous one? Write your ideas in the box below.

Solve for ten. $-\frac{1}{2}>-12x$

[exercise-area rows="i″][/exercise-surface area]
[reveal-reply q="811465″]Prove Solution[/reveal-answer]
[hidden-answer a="811465″]

This inequality has the variable on the right hand side, which is dissimilar from the previous examples. Kickoff the solution process as before, and at the cease, you tin move the variable to the left to write the terminal solution.

Separate both sides by $-12$ to isolate the variable. Since you are dividing by a negative number, you demand to change the management of the inequality sign.

$\displaystyle\begin{array}{l}-\frac{1}{2}\gt{-12x}\\\\\frac{-\frac{1}{2}}{-12}\gt\frac{-12x}{-12}\\\cease{array}$

Dividing a fraction past an integer requires you to multiply by the reciprocal, and the reciprocal of $\frac{1}{-12}$

$\displaystyle\begin{array}{r}\left(-\frac{1}{12}\right)\left(-\frac{1}{2}\right)\lt\frac{-12x}{-12}\,\,\\\\ \frac{ane}{24}\lt\frac{\cancel{-12}10}{\abolish{-12}}\\\\ \frac{1}{24}\lt{x}\,\,\,\,\,\,\,\,\,\,\terminate{assortment}$

Answer

Inequality: $x\gt\frac{i}{24}$. Writing the inequality with the variable on the left requires a piffling thinking, but helps you write the interval and draw the graph correctly.

Interval: $\left(\frac{1}{24},\infty\right)$

Graph: $Open dot on zero with a line through all numbers greater than zero.$

[/hidden-answer]

The following video gives examples of how to solve an inequality with the multiplication holding of equality where the variable is on the right hand side.

$Thumbnail for the embedded element "Ex: Solve One Step Linear Inequality by Dividing (Variable Right)"$

A YouTube chemical element has been excluded from this version of the text. Yous tin view it online here: pb.libretexts.org/ba/?p=52

Combine backdrop of inequality to solve algebraic inequalities

A popular strategy for solving equations, isolating the variable, also applies to solving inequalities. By adding, subtracting, multiplying and/or dividing, you tin rewrite the inequality and then that the variable is on one side and everything else is on the other. Equally with ane-step inequalities, the solutions to multi-step inequalities can be graphed on a number line.

Example

Solve for p. $4p+5<29$

[reveal-respond q="211828″]Bear witness Solution[/reveal-answer]
[hidden-answer a="211828″]

Begin to isolate the variable by subtracting 5 from both sides of the inequality.

$\displaystyle \begin{array}{fifty}4p+5<\,\,\,29\\\underline{\,\,\,\,\,\,\,\,\,-5\,\,\,\,\,-v}\\4p\,\,\,\,\,\,\,\,\,<\,\,24\,\,\end{array}$

Divide both sides of the inequality by 4 to limited the variable with a coefficient of ane.

$\begin{array}{l}\underline{4p}\,<\,\,\underline{24}\,\,\\\,4\,\,\,\,<\,\,four\\\,\,\,\,\,p<vi\cease{array}$

Answer

Inequality: $p<6$

Interval: $\left(-\infty,6\right)$

Graph: Note the open circumvolve at the end point 6 to prove that solutions to the inequality do not include six. The values where p is less than half-dozen are institute all along the number line to the left of half-dozen.

$Number line. Open circle on 6. Highlight on every number less than 6.$

[/hidden-reply]

Bank check the solution.
[reveal-answer q="291597″]Bear witness Solution[/reveal-answer]
[subconscious-respond a="291597″]

Check the end bespeak 6 in the related equation.

$\displaystyle \begin{array}{r}4p+5=29\,\,\,\\\text{Does}\,\,\,4(vi)+5=29?\\24+5=29\,\,\,\\29=29\,\,\,\\\text{Yes!}\,\,\,\,\,\,\end{assortment}$

Effort some other value to cheque the inequality. Permit's employ $p=0$.

$\displaystyle \begin{array}{r}4p+5<29\,\,\,\\\text{Is}\,\,\,4(0)+5<29?\\0+5<29\,\,\,\\5<29\,\,\,\\\text{Yes!}\,\,\,\,\,\end{array}$

$4p+5<29$

[/hidden-answer]

Instance

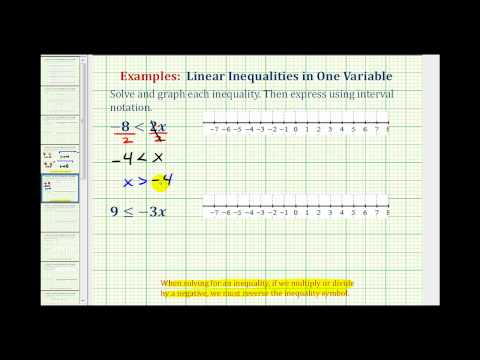
Solve for ten: $3x–seven\ge 41$
[reveal-answer q="238157″]Evidence Solution[/reveal-answer]
[hidden-answer a="238157″]

Brainstorm to isolate the variable by adding seven to both sides of the inequality, then split up both sides of the inequality past 3 to express the variable with a coefficient of ane.

$\displaystyle \begin{array}{50}3x-seven\ge 41\\\underline{\,\,\,\,\,\,\,+7\,\,\,\,+7}\\\frac{3x}{three}\,\,\,\,\,\,\,\,\ge \frac{48}{iii}\\\,\,\,\,\,\,\,\,\,\,x\ge 16\stop{array}$

Respond

Inequality: $x\ge 16$

Interval: $\left[16,\infty\right)$

Graph: To graph this inequality, you draw a airtight circumvolve at the stop point 16 on the number line to show that solutions include the value 16. The line continues to the right from sixteen because all the numbers greater than 16 will also make the inequality $3x–seven\ge 41$ truthful.
$Closed dot on 16, line through all numbers greater than 16.$

[/hidden-answer]

Check the solution.
[reveal-answer q="437341″]Show Solution[/reveal-answer]

[hidden-respond a="437341″]

Offset, check the end bespeak sixteen in the related equation.

$\displaystyle \begin{array}{r}3x-seven=41\,\,\,\\\text{Does}\,\,\,three(16)-7=41?\\48-vii=41\,\,\,\\41=41\,\,\,\\\text{Yes!}\,\,\,\,\,\end{array}$

And then, try some other value to bank check the inequality. Let's utilise $x = 20$.

$\displaystyle \begin{array}{r}\,\,\,\,3x-7\ge 41\,\,\,\\\text{Is}\,\,\,\,\,3(20)-vii\ge 41?\\60-vii\ge 41\,\,\,\\53\ge 41\,\,\,\\\text{Yep!}\,\,\,\,\,\end{array}$

[/hidden-respond]

When solving multi-step equations, pay attention to situations in which you multiply or divide by a negative number. In these cases, you must reverse the inequality sign.

Example

Solve for p. $−58>fourteen−6p$

[reveal-answer q="424351″]Show Solution[/reveal-reply]
[hidden-answer a="424351″]

Note how the variable is on the right hand side of the inequality, the method for solving does not change in this case.

Begin to isolate the variable by subtracting 14 from both sides of the inequality.

$\displaystyle \begin{array}{l}−58\,\,>14−6p\\\underline{\,\,\,\,\,\,\,\,\,\,\,\,-14\,\,\,\,\,\,\,-14}\\-72\,\,\,\,\,\,\,\,\,\,\,>-6p\end{array}$

Split both sides of the inequality past $−half dozen$ to express the variable with a coefficient of ane. Dividing past a negative number results in reversing the inequality sign.

$\begin{array}{l}\underline{-72}>\underline{-6p}\\-half-dozen\,\,\,\,\,\,\,\,\,\,-6\\\,\,\,\,\,\,12\lt{p}\stop{array}$

We tin can also write this as $p>12$. Notice how the inequality sign is nonetheless opening up toward the variable p.

Answer

Inequality: $\left(12,\infty\correct)$
Graph: The graph of the inequality p > 12 has an open circle at 12 with an pointer stretching to the right.

$Number line. Open circle on 12. Highlight on all numbers over 12.$

[/hidden-answer]

Check the solution.
[reveal-respond q="500309″]Show Solution[/reveal-answer]
[hidden-reply a="500309″]

First, check the cease point 12 in the related equation.

$\begin{array}{r}-58=14-6p\\-58=14-6\left(12\correct)\\-58=fourteen-72\\-58=-58\end{assortment}$

Then, try some other value to check the inequality. Try 100.

$\brainstorm{assortment}{r}-58>xiv-6p\\-58>fourteen-six\left(100\right)\\-58>14-600\\-58>-586\end{array}$

[/hidden-answer]

In the following video, y'all will see an case of solving a linear inequality with the variable on the left side of the inequality, and an case of switching the management of the inequality after dividing past a negative number.

$Thumbnail for the embedded element "Ex: Solve a Two Step Linear Inequality (Variable Left)"$

A YouTube element has been excluded from this version of the text. You tin can view it online hither: pb.libretexts.org/ba/?p=52

In the following video, yous will come across an example of solving a linear inequality with the variable on the right side of the inequality, and an example of switching the direction of the inequality after dividing by a negative number.

$Thumbnail for the embedded element "Ex: Solve a Two Step Linear Inequality (Variable Right)"$

A YouTube element has been excluded from this version of the text. Y'all can view it online hither: lead.libretexts.org/ba/?p=52

Simplify and solve algebraic inequalities using the distributive holding

Every bit with equations, the distributive property can be applied to simplify expressions that are part of an inequality. One time the parentheses have been cleared, solving the inequality will exist straightforward.

Example

Solve for ten. $2\left(3x–5\right)\leq 4x+six$

[reveal-respond q="587737″]Show Solution[/reveal-reply]
[subconscious-answer a="587737″]

Distribute to articulate the parentheses.

$\displaystyle \begin{array}{r}\,2(3x-5)\leq 4x+6\\\,\,\,\,6x-10\leq 4x+6\end{array}$

Subtract 4x from both sides to get the variable term on one side only.

$\begin{assortment}{r}6x-10\le 4x+6\\\underline{-4x\,\,\,\,\,\,\,\,\,\,\,\,\,\,-4x}\,\,\,\,\,\,\,\,\,\\\,\,\,2x-ten\,\,\leq \,\,\,\,\,\,\,\,\,\,\,\,6\finish{array}$

Add 10 to both sides to isolate the variable.

$\begin{array}{r}\\\,\,\,2x-10\,\,\le \,\,\,\,\,\,\,\,six\,\,\,\\\underline{\,\,\,\,\,\,+ten\,\,\,\,\,\,\,\,\,+10}\\\,\,\,2x\,\,\,\,\,\,\,\,\,\,\,\le \,\,\,\,\,xvi\,\,\,\end{array}$

Divide both sides by 2 to express the variable with a coefficient of 1.

$\brainstorm{assortment}{r}\underline{2x}\le \,\,\,\underline{16}\\\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,two\,\,\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,10\,\,\,\le \,\,\,\,\,8\terminate{assortment}$

Answer

Inequality: $\left(-\infty,viii\correct]$
Graph: The graph of this solution set includes 8 and everything left of viii on the number line.

$Number line with the interval (-oo,8] graphed$

[/hidden-answer]

Check the solution.
[reveal-answer q="808701″]Show Solution[/reveal-reply]
[hidden-answer a="808701″]

Offset, bank check the end betoken 8 in the related equation.

$\displaystyle \begin{array}{r}2(3x-5)=4x+half dozen\,\,\,\,\,\,\\two(iii\,\cdot \,eight-5)=4\,\cdot \,eight+vi\\\,\,\,\,\,\,\,\,\,\,\,ii(24-v)=32+6\,\,\,\,\,\,\\ii(19)=38\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\38=38\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}$

So, choose another solution and evaluate the inequality for that value to brand certain it is a true argument. Try 0.

$\displaystyle \begin{array}{l}2(iii\,\cdot \,0-5)\le 4\,\cdot \,0+6?\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2(-5)\le 6\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-10\le six\,\,\cease{assortment}$

$\left(-\infty,eight\right]$

[/hidden-answer]

In the following video, you are given an example of how to solve a multi-stride inequality that requires using the distributive holding.

$Thumbnail for the embedded element "Ex: Solve a Linear Inequality Requiring Multiple Steps (One Var)"$

A YouTube chemical element has been excluded from this version of the text. You lot tin view information technology online hither: pb.libretexts.org/ba/?p=52

Think About It

In the next case, yous are given an inequality with a term that looks complicated. If you lot pause and think about how to use the club of operations to solve the inequality, it will hopefully seem similar a straightforward problem. Apply the textbox to write down what y'all think is the best showtime step to accept.

Solve for a. \(\displaystyle\frac

ParseError: EOF expected (click for details)

Callstack:     at                        (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/01:_Solving_Equations_and_Inequalities/1.05:_Solve_Inequalities), /content/body/div[7]/div/div/div[3]/div/p[2]/span[1], line i, cavalcade 2

half-dozen{<2}\)

[practice-area rows="one″][/practice-area]

[reveal-answer q="701072″]Prove Solution[/reveal-reply]

[hidden-answer a="701072″]

Clear the fraction by multiplying both sides of the equation by 6.

\(\displaystyle \begin{array}{r}\frac

ParseError: EOF expected (click for details)

Callstack:     at                        (Courses/Lumen_Learning/Book:_Beginning_Algebra_(Lumen)/01:_Solving_Equations_and_Inequalities/i.05:_Solve_Inequalities), /content/body/div[7]/div/div/div[three]/div/p[7]/bridge[1], line ane, column ii

6{<ii}\,\,\,\,\,\,\,\,\\\\six\,\cdot \,\frac{2a-four}{6}<2\,\cdot \,half-dozen\\\\{2a-four}<12\,\,\,\,\,\,\end{assortment}\)

Add 4 to both sides to isolate the variable.

$\displaystyle \begin{array}{r}2a-iv<12\\\underline{\,\,\,+four\,\,\,\,+four}\\2a<16\end{array}$

Divide both sides by 2 to express the variable with a coefficient of i.

$\displaystyle \brainstorm{array}{c}\frac{2a}{2}<\,\frac{16}{2}\\\\a<8\end{array}$

Respond

Inequality: $a<eight$

Interval: $\left(-\infty,8\right)$

Graph: The graph of this solution contains a solid dot at 8 to show that 8 is included in the solution set. The line continues to the left to show that values less than 8 are also included in the solution set up. $Open circle on 8 and line through all numbers less than 8.$

[/hidden-reply]

Check the solution.
[reveal-answer q="905072″]Show Solution[/reveal-answer]

[hidden-answer a="905072″]
First, bank check the stop bespeak 8 in the related equation.

$\displaystyle \begin{array}{r}\frac{2a-4}{six}=2\,\,\,\,\\\\\text{Does}\,\,\,\frac{2(8)-iv}{6}=2?\\\\\frac{sixteen-4}{half dozen}=2\,\,\,\,\\\\\frac{12}{six}=2\,\,\,\,\\\\2=ii\,\,\,\,\\\\\text{Aye!}\,\,\,\,\,\end{array}$

Then choose some other solution and evaluate the inequality for that value to make sure it is a true argument. Try 5.

$\displaystyle \brainstorm{array}{r}\text{Is}\,\,\,\frac{2(5)-4}{6}<2?\\\\\frac{x-4}{6}<ii\,\,\,\\\\\,\,\,\,\frac{six}{six}<2\,\,\,\\\\one<2\,\,\,\\\\\text{Yep!}\,\,\,\,\,\end{array}$

[/hidden-reply]

Summary

Solving inequalities is very similar to solving equations, except you have to opposite the inequality symbols when you multiply or divide both sides of an inequality by a negative number. There are three ways to represent solutions to inequalities: an interval, a graph, and an inequality. Considering at that place is normally more than than ane solution to an inequality, when you lot check your answer you should check the end betoken and one other value to check the direction of the inequality.

Inequalities can take a range of answers. The solutions are often graphed on a number line in order to visualize all of the solutions. Multi-step inequalities are solved using the same processes that piece of work for solving equations with ane exception. When you multiply or divide both sides of an inequality by a negative number, y'all must reverse the inequality symbol. The inequality symbols stay the same whenever yous add or subtract either positive or negative numbers to both sides of the inequality.